T3 - Relación Grupo y Sexo en los grupos de Google Apps y Moodle

Desgloso a continuación la solución de mi tarea evaluable T3, en donde se pide:

I. Reflexión sobre la relación entre las variables: calificación, grupo y sexo

Observé que no existe una diferencia significativa en las calificaciones en los grupos de Moodle y Google Apps y en los sexos.

II. Gráfica de Interacción

1. Primero se procede a cargar los datos del archivo #3, como es una archivo csv, delimitado por punto y coma (;), procedemos a importarlo desde el menú datos en la opción importar archivo de texto.
2. Filtramos la tabla con las cabeceras grupo y sexo desde el menú de datos de excel.
3. Aplicamos la formula sobre el filtro =SUBTOTALES(1;C2:C41), la que nos permite  según el filtro saber el promedio de los datos.
4. Creamos a partir de los filtros las tablas y los  gráficos de interacción.

1.1 Gráfico de Interacción:  Sexo - Grupo

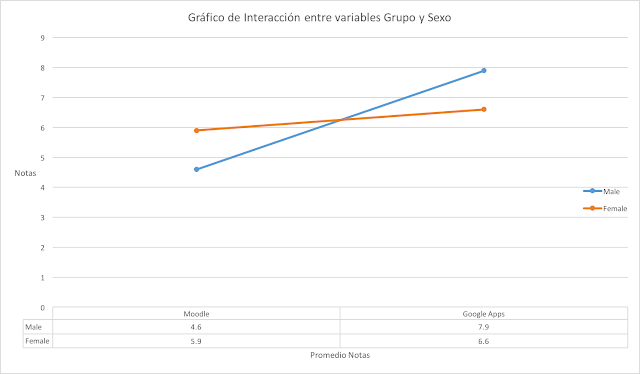
1.2 Gráfico de Interacción:  Grupo - Sexo

1.3 Gráfico Media Notas por Sexo

1.4 Gráfico Media Notas por Grupo

• Análisis:  Observando la gráfica de interacción (1.2) se nota que los del sexo masculino obtienen mejor calificación si usan Google Apps, a diferencia de los que que usaron Moodle. Sin embargo el resultado obtenido por el sexo femenino es muy cercano en ambas plataformas.

III. Análisis en R-Studio de significado estadístico entre las calificaciones según grupo y sexo

1.5 Tablas creadas en R, a partir del archivo

Carga de datos:

• dataYear3 <- read.csv("~/Downloads/Notas-2grupos-v3.csv", sep=";")

Filtrado:

• dataYear3GoogleApps <- subset(dataYear3,grupo=="Google Apps"), creación de la tabla del grupo Google Apps.
• dataYear3Moodle <- subset(dataYear3,grupo=="Moodle"), tabla correspondiente al grupo de Moodle.
• dataYear3F <- subset(dataYear3,sexo=="F"), tabla correspondiente al sexo femenino
• dataYear3M <- subset(dataYear3,sexo=="M"), creación de la tabla del sexo masculino.

Análisis:

Variable sexo

Al aplicar el comando t.test, para el sexo, los resultados son idénticos, por lo que podemos afirmar que el sexo no constituye una diferencia estadística significativa para las calificaciones de los estudiantes.

1.6 Gráfica con comando t.test aplicado al Sexo y  su resultado 

Variable grupo

Aplicado entonces para la variable grupo, el comando t.test y nos indica que los estudiantes que utilizaron Google Apps, obtuvieron mejor calificación que los que usaron Moodle.  Los de Google Apps obtuvieron 2 puntos (en base a 10) por encima del grupo de Moodle.

1.7 Gráfica con comando t.test aplicado al grupo y  su resultado 

IV.Análisis de la función aov() de R, de la interacción estadística entre las variables grupo y sexo

Al realizar el comando aov() con los datos del archivo, se verifica que existe una interacción estadísticamente significativa para las variables grupo y sexo con relación a la calificación ver gráfico 1.8.    

1.8 Gráfica con comando aov() en las variables grupo y sexo y  su resultado 

Esto se observa con el valor obtenido presente en el Pr(>F) 7.74e-05, es decir 0.0000774 (0.0074%), que representa un valor muy por debajo del 5%.

Por último, utilizando el comando attach(), el cual me permitió asignar los datos de tabla general (dataYear3), y luego usarlos para graficar con el  comando interaction.plot, ver gráfico 1.9.

Comandos aplicados:    attach(dataYear3)  y luego interaction.plot(grupo, sexo, nota)

Que generaron el gráfico de interacción:

1.9 Gráfica de interacción generada en R, a partir del comando interaction.plot

Documentos consultados:

• Gráficos de interacción 
• R para principiantes